Ferrite Hysteresis Theory: Hysteresis Parameters from Non-Hysteresis Loops
-
2021.11.04
一、概要
本文描述了如何从一组实验磁化测量中获得在磁滞理论中定义磁滞的参数。这些非磁滞参数可以从初始的非磁滞磁化系数,矫顽力 , 剩磁和磁滞回环的顶点坐标中计算出来。从这些实验数据中计算出非磁滞参数是使用磁滞模型过程的关键步骤。
二、介绍
此前,基于对均匀阻碍畴壁运动的考虑,导出了一个描述铁磁磁滞的微分方程[1,2]. 这个公式表示了一个基于物理特性的现象模型,其中非滞回磁化表示为全局能量的最小值,磁化强度想要到达该值,但由于畴壁运动的阻抗而无法达到。以磁场不均匀性和位错的形式出现的畴壁运动的阻抗越大,初始磁化曲线的位移就越大。
磁滞方程可以最简化为两个分量的等式, 分别是可逆和不可逆磁化率:
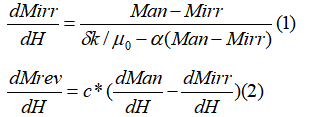
其中钉扎(损耗)系数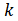 既可以用单位
既可以用单位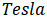 表示,如等式(1);如果
表示,如等式(1);如果 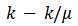 表示为钉扎系数,
表示为钉扎系数, 也可以用单位
也可以用单位 表示, 因为
表示, 因为 可以作为
可以作为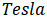 的维数:
的维数: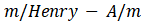 。
。
1、非磁滞磁化强度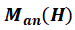
为了提供磁滞方程的解,需要对非磁滞磁化强度 的形式做一些假设。尽管我们尚不知道完全通用的非磁滞方程,但修改后的Langevin函数已经证明可以成功适用。
的形式做一些假设。尽管我们尚不知道完全通用的非磁滞方程,但修改后的Langevin函数已经证明可以成功适用。
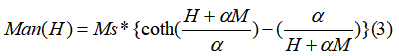
通过上述方程式,在 B、H 平面原点处的非磁滞曲线的斜率可以表示为:

该公式对α 和a 的取值范围做出了约束。
2、正常磁滞曲线的初始斜率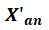
可逆磁化分量可以用公式(2)的参数c表示。目前使用的这些方程的数值解和原始版本[2]中略有不同 , 在本例中表示为:
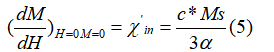
3、矫顽力和最大微分磁化率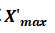
矫顽力是由损耗参数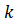 决定。对于非常软的磁性材料,如果
决定。对于非常软的磁性材料,如果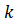 和
和 是用同一个单位测量的,则
是用同一个单位测量的,则
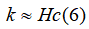
然而 , 当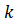 和
和 变得更大的时候,这个简单的公式关系就不再精确,要用下列公式替代:
变得更大的时候,这个简单的公式关系就不再精确,要用下列公式替代:

在其他非磁滞参数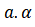 和
和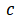 已知的情况下 , 这个公式可以用矫顽力
已知的情况下 , 这个公式可以用矫顽力 和最大微分磁化率
和最大微分磁化率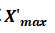 来计算
来计算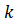 值。
值。
4、剩磁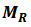 和剩磁的微分磁化率
和剩磁的微分磁化率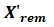
通常我们用公式(7)去第一次尝试计算k的时候不知道参数 α 和 a , 因为初始点非磁滞曲线的斜率只给出了α和a的关系。因此需要引入另外的信息,磁滞曲线中下一个最重要的点就是剩磁。在这个点上,磁滞公式可以表示为 :

这个公式可以对剩磁参数提供必要的约束。
除了上述“不动点“外,我们还发现具有最大振幅的磁滞回路的环路尖端的坐标可以用作磁滞参数计算的额外约束条件。
三、结果
这个算法最重要的第一个测试就是在已知参数 生成的磁滞曲线的情况下,通过运用方程(4)(5)(7)(8)中的各种微分磁化率和截距能否正确地求解出这些参数。
生成的磁滞曲线的情况下,通过运用方程(4)(5)(7)(8)中的各种微分磁化率和截距能否正确地求解出这些参数。
两个参照磁滞曲线的例子以及用于生成这两个曲线的参数值分别显示在图1和图2中。通过(4)(5)(7)(8)的方程计算求得的参数值和回环顶点的坐标一起显示在表1中。

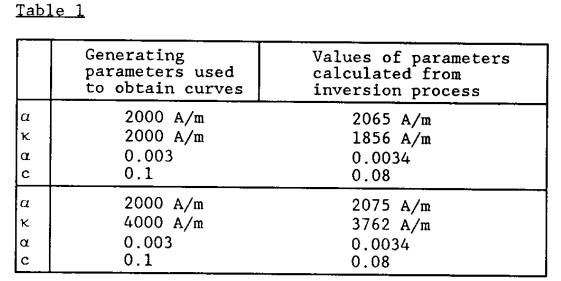

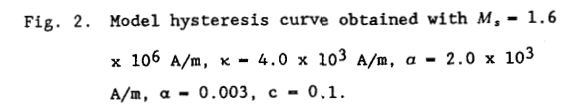
四、结论
本文描述了一种反演过程,即利用磁滞理论从选定的斜率和磁滞曲线上的截距计算出生成模型滞后回路所需的参数。该算法是对磁滞建模多年实验的结果,在大多数情况下,参数确定的误差都在百分点以内。
引用:
[l] D. C. Jiles and D. L. Atherton, J. Appl. Phys.,
55, 2115, 1984.
[2] D. C. Jiles and D. L. Atherton, J. Mag. Mag.
Mater., 61, 48, 1986.
欢迎点击 软件试用 申请试用我们的软件,过程中的任何疑问可联系support技术人员,期待与您的交流!
本文转载并翻译自IEEE官网,部分图片来自网络,如有侵权,请联系删除,谢谢!
Recommended
-
 Process Corners and Applications in IBIS Modeling2025.04.23
Process Corners and Applications in IBIS Modeling2025.04.23 -
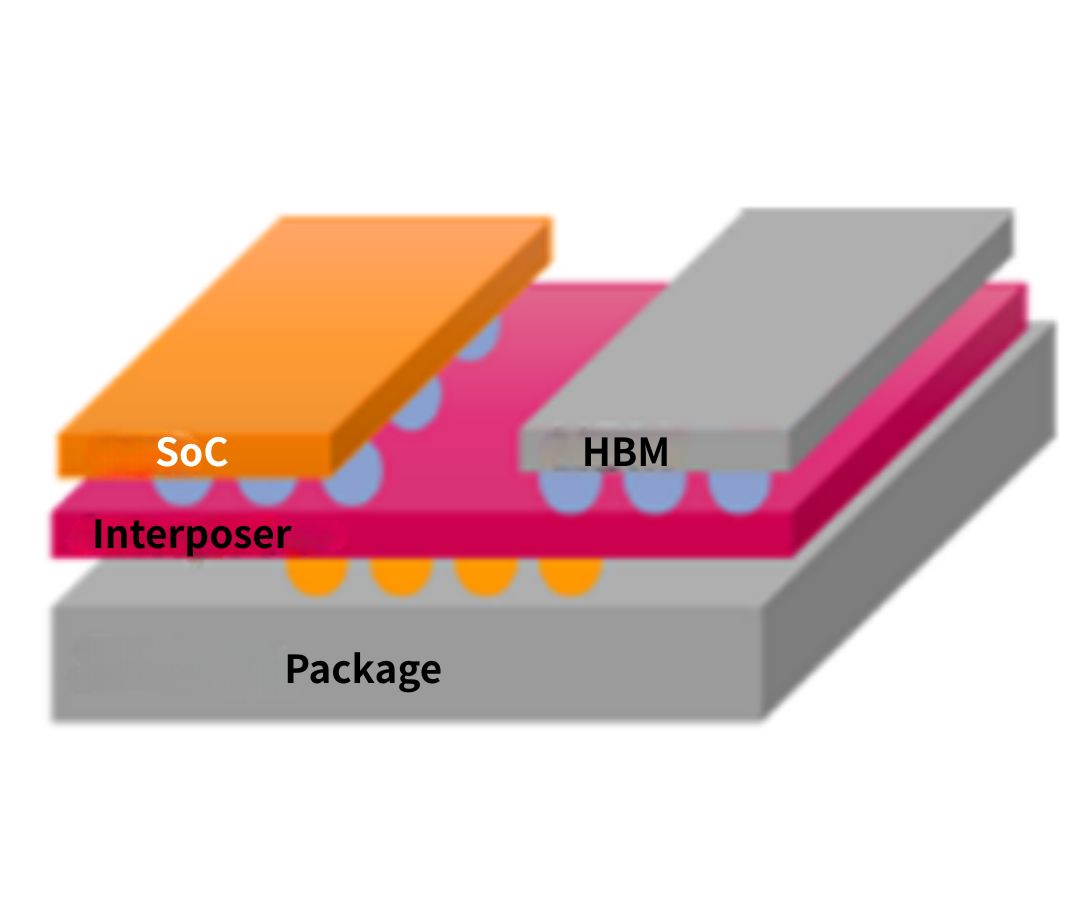
 Technical Synergy of Chiplet and Advanced Packaging and Challenges for EDA Simulation Tools (II)2025.04.21
Technical Synergy of Chiplet and Advanced Packaging and Challenges for EDA Simulation Tools (II)2025.04.21 -
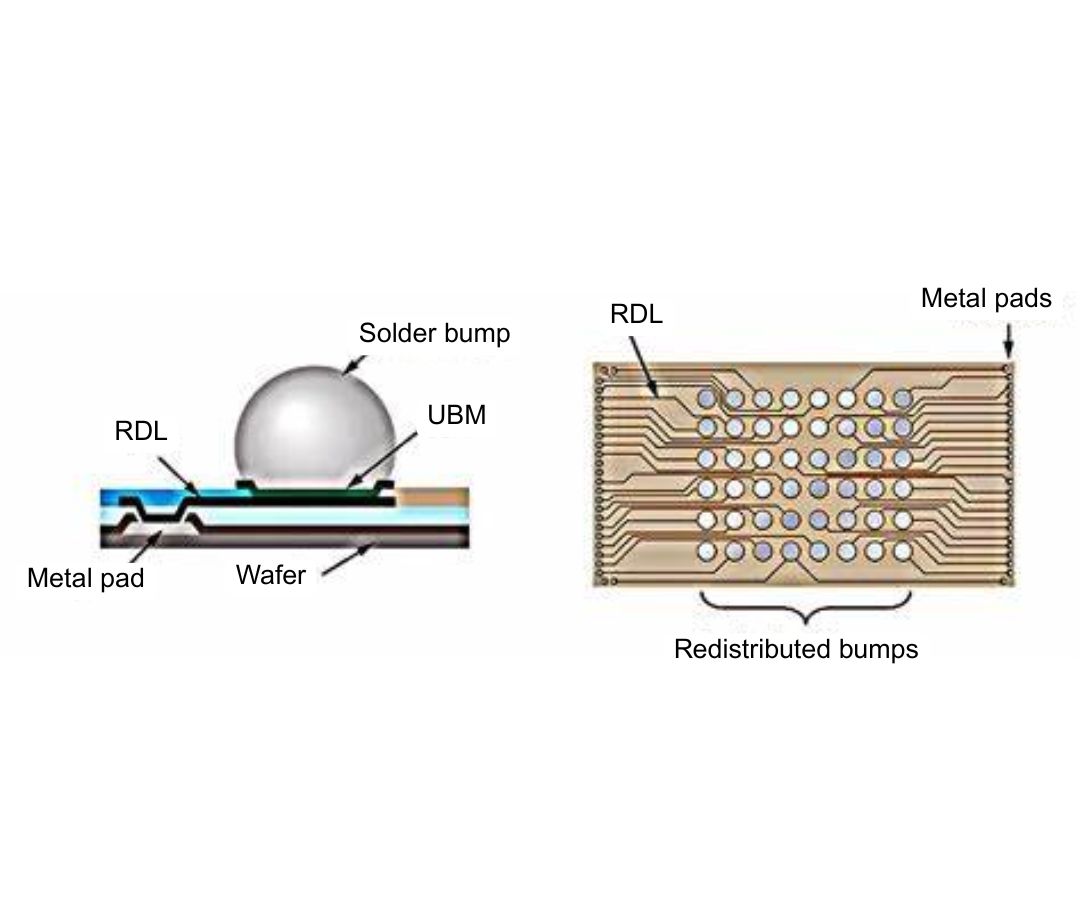
 Technical Synergy of Chiplet and Advanced Packaging and Challenges for EDA Simulation Tools (I)2025.04.11
Technical Synergy of Chiplet and Advanced Packaging and Challenges for EDA Simulation Tools (I)2025.04.11 -
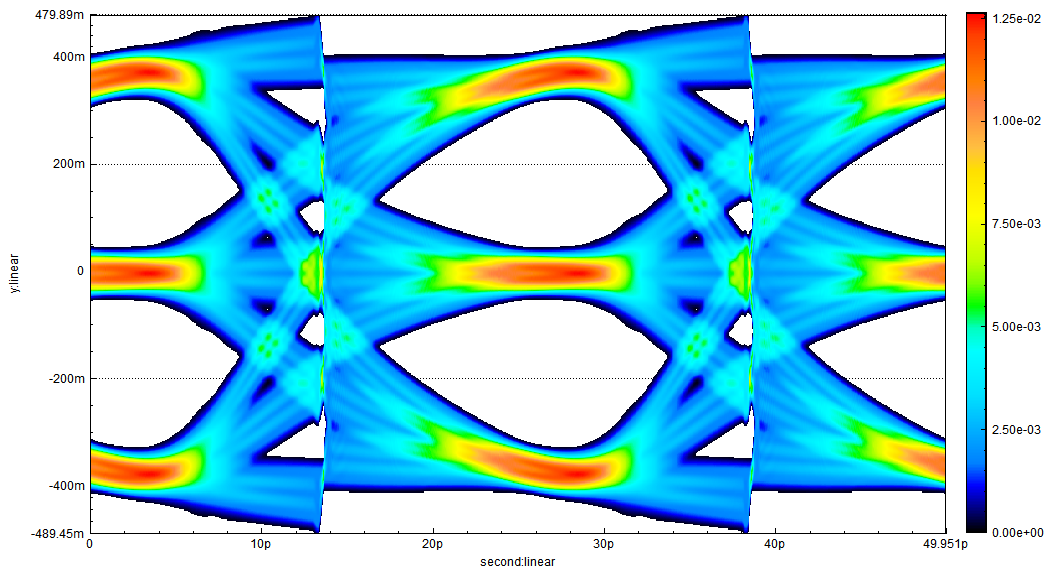
 PAM3 Encoding and Simulating Verification in High-Speed Transmission2025.03.31
PAM3 Encoding and Simulating Verification in High-Speed Transmission2025.03.31