基于实验设计和机器学习的快速多边响应方法

摘要：多边沿响应(MER)方法可以准确捕捉信号完整性仿真中的非线性特征。然而，瞬态仿真要获得高阶MER的所有边缘响应是很耗时的。本文提出了一种基于实验设计（DoE）和机器学习的快速方法来获取严重非线性链路的所有边缘响应。DoE 用于为人工神经网络 (ANN) 生成一些训练集。ANN使用生成的训练集来构建精确的模型。构建好的 ANN 模型用来预测剩余的边缘响应。本文所提出的方法只需要9.8分钟即可获得所有多边沿响应，同样情况下，对于9阶的MER来说，使用瞬态仿真需要 92 分钟才可获得全部多边沿响应。结果表明，本文所提出的方法与实际测量值之间的眼高和眼宽误差小于5%。

关键词：实验设计，机器学习，多边响应，非线性高速链路

一、介绍 

随着数字系统数据速率和集成密度的不断增加，高速链路中已经产生了越来越严重的非线性效应。因此，通信工程师不得不通过大量的瞬态仿真来评估系统性能。然而，瞬态仿真非常耗时。近年来出现了各种快速时域仿真方法来实现高效评估高速链路性能的目的，例如基于单位响应(SBR)的方法[1-3]、双边沿响应(DER)的方法[4-5]和基于多边响应 (MER)的方法[6-8]。SBR和DER方法模拟非线性驱动器效应的能力有限。MER方法的原理是根据前面的位模式构造多个上升沿和下降沿，可以用来捕获非线性行为。此外，对于严重非线性的高速链路，增加MER阶数可以提高精度。然而，增加MER阶数需要更多的边缘响应。例如，一个十阶的MER需要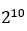个分别具有不同初始模式的上升沿和下降沿响应。边缘响应通常通过瞬态仿真获得，因此确定高阶MER的所有边缘响应是一项挑战。

人工神经网络（ANN）具有很强的学习能力和强大的非线性映射能力，因此近年来被广泛应用于对高速系统的建模和仿真分析[9-13]。给定足够数量的训练集，ANN可以精确地模拟非线性链路的行为。然而，使用数量很少的训练集来制定准确的ANN模型是一项具有挑战性的工作。

本文提出了一种基于实验设计（DoE）[14-15]和多层感知器（MLP）的方法，用来获得高阶MER所有边沿响应。DoE用于为MLP生成一些最佳训练模式，然后对这些训练模式执行瞬态仿真以获得相应的边缘响应。使用瞬态仿真训练集构建用于预测剩余边缘响应的MLP。最后，将预测得到的边缘响应叠加以生成眼图，并通过实验测量进行验证。

二、基于 DOE 和 MLP 的快速MER 方法

对于具有二级系数的实验，需要执行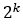来分析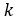系数的影响以及这些系数之间的相互作用对最终实验结果的影响。当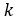的数值非常大时，运行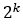的成本是巨大的。因此，使用DoE方法可以获得理想的实验结果，并通过优化设计执行相对较少的运行次数得出科学结论[14-15]。

DoE 的矩阵公式如下：                            

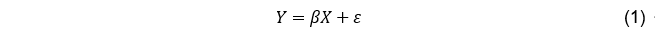
其中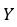是输出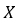，是输入矩阵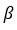，是未知参数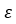，是误差，即一个正态分布的随机变量。第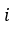次运行的X和Y之间的关系通常可以通过多元线性回归模型进行预测。高速链路非线性的先决条件包含交互项。其表达式如下：           

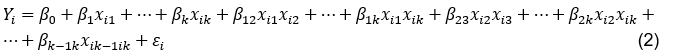
下面给出了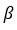的最小二乘估计量:   

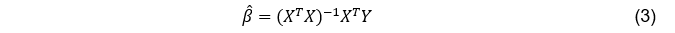
的方差-协方差矩阵为： 

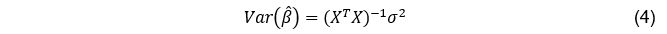
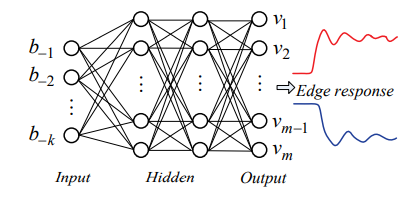
图1. 非线性链路的ANN模型

方差-协方差矩阵的行列式越小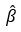，越接近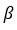。方差误差值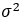设置为1。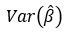行列式的最小值可以使用D-optical设计，最大化矩阵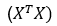的行列式来获得。

考虑到高阶MER前k个bit位的影响，需要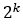个上升沿响应和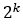个下降沿响应与之对应。具有k个二级参数的DoE用于筛选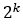个模式中的些许位模式。选定的位模式用作人工神经网络的训练数据输入集。对应于这些选定模式的边缘响应是通过瞬态仿真获得的，并用作训练数据输出集来构建非线性链路的ANN模型。构建的ANN模型用于高效预测其他模式的边缘响应。

图1展示了本文中对非线性链路进行建模的MLP模型。神经网络由1个输入层、2 个隐藏层和1个输出层组成。MER的前k个bit位用作训练集的输入，并表示为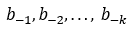表示第k阶MER。输入位模式的响应作为训练集的输出。例如，如果响应由250个单位间隔(UIs)组成，每个UI有100个样本，则输出层中有25000个单元，每个单位代表边缘响应的一个样本电压，表示为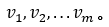每个隐藏层有90个隐藏单元，最小成本函数的正则化系数为0.008，反向传播（BP）算法用于优化每个感知器的权重，Adam算法用于最小化成本函数，Tanh函数用于激活函数。以同样的方式经过15000次迭代后构建了两个MLP模型：一个模型预测上升沿响应，另一个模型预测下降沿响应。

三、验证所提出的方法

本节中，通过对传输线实测数据的对比，验证本文所提出方法是否高效可行。

A．测量准备

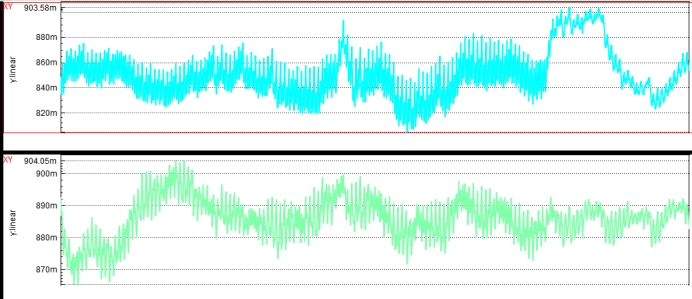
如图2所示，使用任意波形发生器 (AWG) 为信道提供激励，使用示波器测试系统响应。为了模拟有源发射机的非线性行为，我们首先在Simulink中仿真获得非线性发射机的输出样本[16]，然后将样本数据导入AWG并设置同样的非线性条件。Tx端激励信号的幅值为±0.8 V，频率为3 Gbps，上升和下降时间为42 p秒。

图2.实验设置，A是任意波形发生器，B是信道，C是示波器

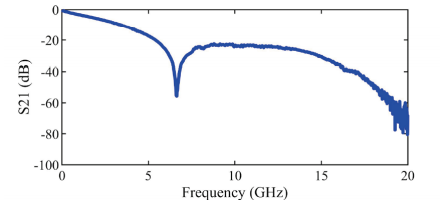
图3.被测传输线的传输系数

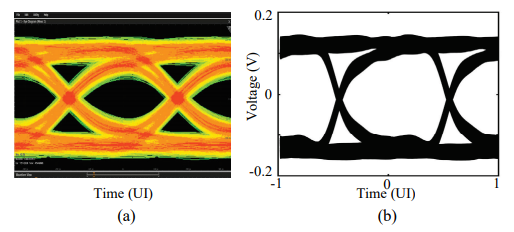
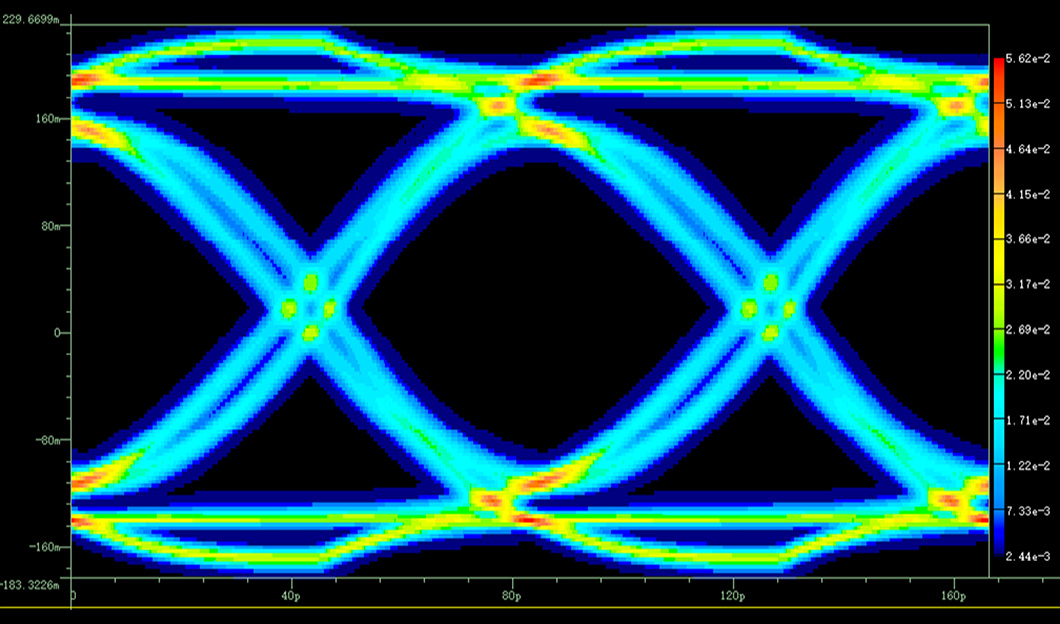
图4.通过(a)测量和(b)三阶MER叠加得到的PRBS眼图

通信信道的传输系数由图3给出，示波器生成的PRBS眼图由图4(a)给出，与示波器设置相同的PRBS通过三阶MER叠加得到的眼图由图4(b)给出。我们可以看到，这两个眼图在形状和高度上都有很大差异。这一结果反映出波形具有非常明显的非线性，因此三阶的MER不能准确捕捉实际输出信号的特性。通过遍历仿真，我们发现九阶的MER可以获得准确的结果，但是9阶的MER所需要进行的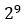个上升沿和下降沿的瞬态仿真的计算量极为庞大。

使用DoE方法选择几个位模式，随后对其响应进行测量。选择的位模式和相应的响应被用作训练数据集来构建MLP模型。构建的MLP模型用于预测剩余的边缘响应。

B．验证本文方法的效率

通过比较由DoE随机或者统一选择的MLP训练数据集，在三种不同情况下测量和模拟得到的眼图，来验证本文所提出方法的可行性。使用DoE算法为本文所提方法选择16个训练模式和8个测试模式。

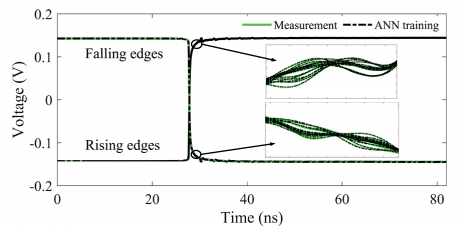
图5. 测量的边缘响应与人工神经网络预测的边缘响应的比较

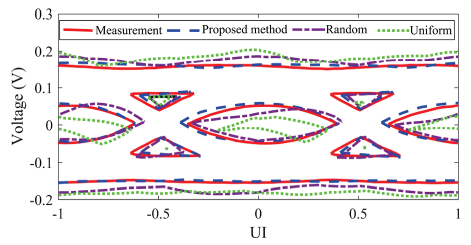
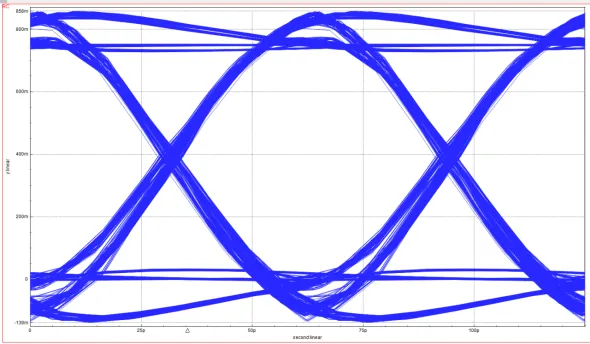
图6.不同方法得到的眼图

三种情况的十进制训练模式如表一所示。上升沿和下降沿模式分别由前导模式后添加“01”和“10”构成。为了消除ISI（符号间干扰）的影响，我们必须从“前导模式+01”的上升沿模式响应中减去“前导模式+00”的上升沿模式响应。同样，“前导模式+11”的下降沿模式响应必须从“前导模式+10”的下降沿模式响应中扣除。每个响应由250个单位间隔(UI) 组成，每个UI有100个样本。

我们将16个上升沿和16个下降沿模式以及相应的响应用作训练数据集来构建MLP。再通过MLP预测剩余的496个上升沿和下降沿响应。图5是测量得到的边缘响应和由MLP训练结果预测得到的边缘响应之间的对比。可以看到，所有预测的边缘响应都很好地匹配了测量的结果。测量得到的10000 PRBS14的眼图很好地与上升沿和下降沿响应叠加得到的眼图重合。图6比较了模拟预测和实际测量的眼图轮廓。实线表示测量结果，虚线表示使用本文所提出方法的预测结果，点划线和点线分别对应于从个前导模式中随机和均匀选择MLP训练数据集所获得的结果。可以看到，使用文章所提出的方法获得的结果与实测结果最匹配，使用随机选择，特别是均匀选择的方法获得的结果与实测结果存在显著差异。

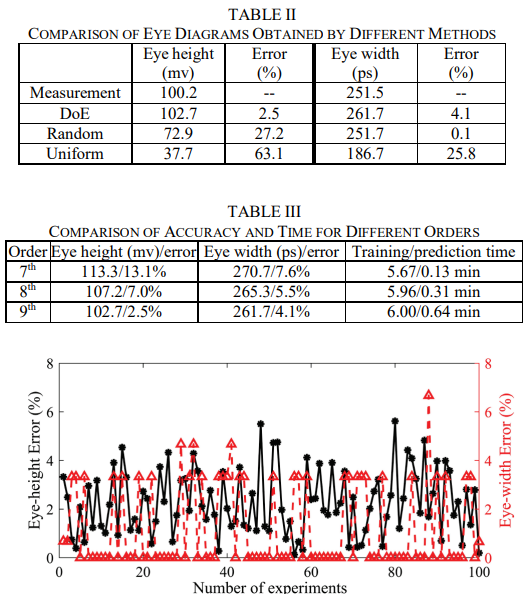
图7.100次DoE实验中眼高和眼宽的误差趋势

测量得到眼图和预测得到的眼图眼高和眼宽之间的误差如表II所示。可以看到，本文所提方法的测误差小于5%，从而验证了该方法的准确性。由于未知原因，模拟结果和测量结果之间总是存在一些偏差。虽然随机法得到的眼宽误差仅为0.1%，但整个眼图轮廓明显偏离了实测得到的眼图轮廓。传统的瞬态仿真需要 92.16 分钟来估计具有 4 GHz CPU 和 8 GB RAM 的计算机上所有的上升沿和下降沿。本文采用的方法，需要0.08分钟使用DoE进行扫描实验，3.08分钟进行16个上升沿和16个下降沿训练模式的瞬态仿真，6分钟进行两次MLP训练，0.64分钟预测剩余的496个上升沿和496个下降沿，对应总共9.8分钟。表III比较了7阶、8阶和9阶MER 的精度和仿真时间。可以看出，9阶的结果与测量结果最接近。模型训练的时间不会随着阶数的增加成比例的增加。

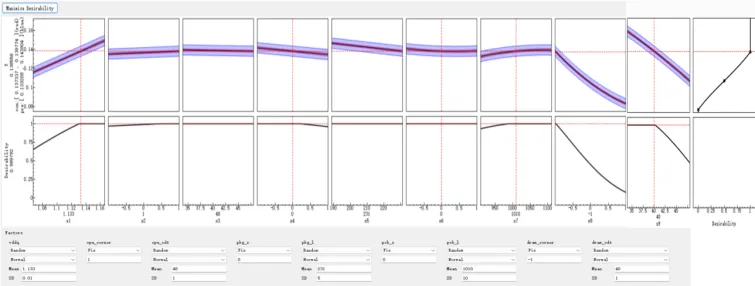
由于DoE方法是随机的，因此额外进行了100次模拟实验以验证该方法的稳定性。眼高和眼宽的误差如图7所示。大多数实验的误差在5%以内，验证了DoE方法的准确性。

四、总结

本文提出了一种基于DoE和MLP快速准确获得非线性高速链路多边缘响应的方法。该方法可以根据DoE为高阶MER选择的一些已知响应快速估计所有的边缘响应。该方法高效准确，可应用于具有明显非线性高速链路的统计和误码率眼图计算。（本文转载自IEEE官网）