Modeling the Influence of Temperature on Hysteresis Effects Based on Jiles-Atherton Theory

摘要：为了了解不同温度下磁材料的磁化过程，需要建立一个温度相关的模型。本研究基于Jiles-Atherton理论建立了一个物理模型来研究温度对磁滞的影响，加入临界指数和居里温度作为附加参数，通过现有模型中受到温度影响的磁滞参数来体现热效应。通过对替代钴铁氧体材料的测量，验证了受温度影响的JA模型的有效性，结果吻合较好。

一、介绍

磁滞是一种磁场现象：无论磁场强度增加还是减少，磁化路径都会在外加磁场的作用下遵循一定规律进行变化。根据Jiles–Atherton（JA）模型[1]，铁磁材料的总磁化强度可以是不可逆磁化分量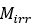和可逆磁化分量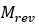之和。

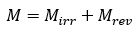（1）

考虑到磁化作用的不可逆分量主要是受到畴壁作用的影响，而可逆磁化分量则受到微观形变中没有能量耗散的畴壁弯曲的影响，磁场中磁化强度的依赖关系可以通过微分方程来表示：

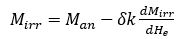（2）

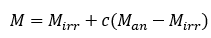（3）

这里的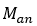是非磁滞磁化强度，它是一个域中矩的能量函数，取决于各向异性可以有不同的形式。对于各向同性材料，表示为：

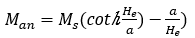（4）

在具有“密度“的域中外加场和磁的相互作用下,有效磁场强度为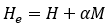，域耦合和域密度影响了磁滞回线的斜率。与钉扎点密度和能量的乘积成正比的微观结构参数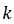是决定磁滞回线矫顽力[2]的主要因素。代表了畴壁弯曲相对作用的可逆系数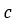是初始磁化率和初始无滞后磁化率的比例。方向系数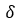在磁场强度增加时+1，在磁场强度H下降时-1。

JA 理论已经扩展到磁弹性效应 [3]、[4] 和各向异性 [5]。之前的理论基于模型参数与实验的拟合数据，致力于扩展具有热效应 [6]、[7]的模型。而本篇则侧重于将微观结构滞后参数作为温度函数来表达，并对由此产生的温度相关的JA 模型与实验曲线进行比较。

二、JA模型的温度效应

温度效应可以通过(2)-(4) 中滞后参数的温度依赖性合并到模型中：自发磁化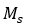，域耦合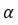 , 钉扎系数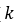以及可逆系数。

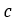A.     自发磁化强度

自发磁化强度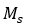的温度依赖性可以用铁磁理论来表示：

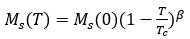（5）

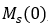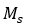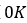是自发磁化强度在时候的值。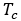是居里温度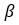，是由平均场定理导出的与物质有关的临界指数。

B.     钉扎系数

在软磁材料中，钉扎系数可以近似的表示为矫顽力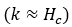。由于铁磁材料的矫顽场呈指数衰减，畴壁钉扎矫顽力系数应该与温度呈指数关系变化：

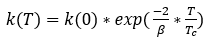 (6)

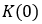是在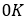的钉扎系数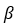，是临界指数参数。

C.    域密度

域密度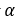虽然是一个明确的温度函数，但只体现出温度上可以忽略不计的变化，因此在该模型中被作为一个常数。

D.    域耦合

域耦合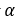，表示畴壁之间磁的相互作用力，在各向同性材料中可以用以下方程表示

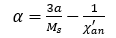（7）

在较高的非磁化率下，第二项对于磁耦合的作用可以忽略不计，因此将表达式根据（5）替换为：

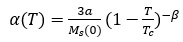（8）

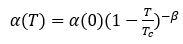（9）

其中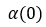是磁耦合在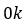时的值，是临界值。

E.     可逆系数

可逆系数的处理方式类似于磁耦合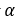，对于各向同异性材料，可以表示为

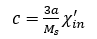（10）

假设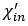为恒定的初始磁化率，替换（5）中的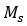的表达式，可以得到：

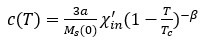（11）

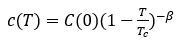（12）

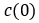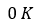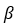其中是可逆系数在时的值，是临界值。

F.     通用识别过程

控制磁化过程的磁滞参数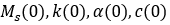和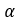可以从磁特性中识别，例如初始磁化率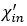、非磁滞磁化率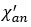、矫顽力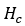和在 0 K 下测量的剩磁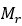。这些过程在论文[11]和[12]中都有详细记录, 足以作为建模的理论依据。通过拟合(5) 中所示的分析模型，使用作为温度函数的测量自发磁化强度来估计临界指数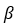和居里点。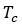

此过程可以确定所有用来描述在任何温度下直至居里点的滞后行为所需要的必要参数。

G.    示例计算

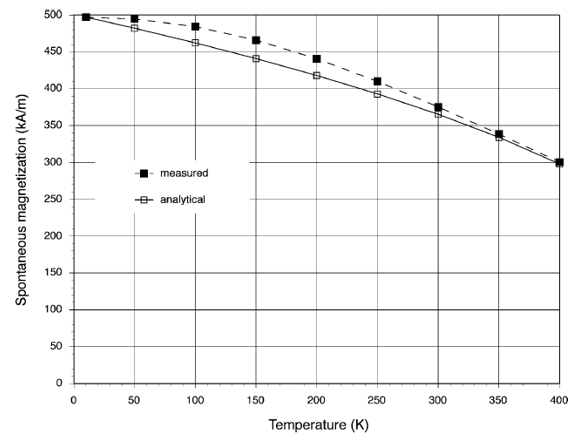
图 1

例如，在确定了必要的磁滞参数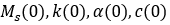和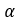之后，如图 1 所示，使用自发磁化强度与温度曲线的对比来确定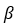和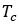。自发磁化强度在 550 K 时迅速下降到零，表明存在从磁有序状态（亚铁磁性）到磁性无序状态（顺磁性）（未显示）。磁滞参数随温度的变化如图 2 所示。在图 2(a) 中，自发磁化强度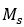随温度升高而减小，并在接近居里点时逐渐迅速下降到零。在图2（b）中，钉扎因子随温度呈指数下降，表明矫顽场呈指数下降[10]。图 2（c）和（d）可以看到，域耦合和可逆性因子随温度单调递增。但是可逆因子在居里点的上限为 1。图 3记录了在 10 K 到 530 K 的温度范围区间内与温度相关的磁滞回线的变化。随着温度向居里点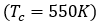升高，磁滞回线趋平，经过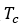后材料变成顺磁性。

三、实验对比

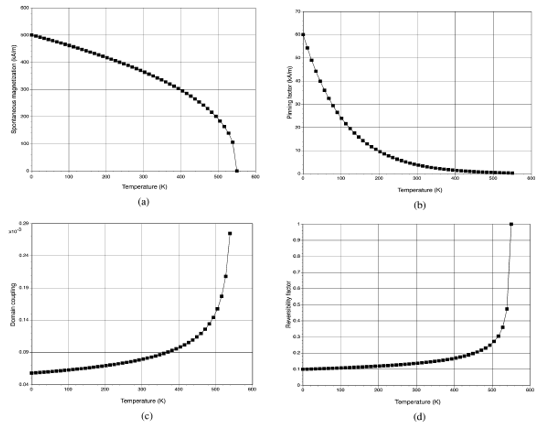
图. 2

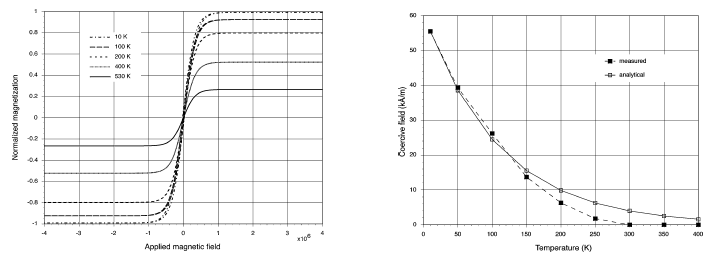
 图. 3                                                                             图. 4

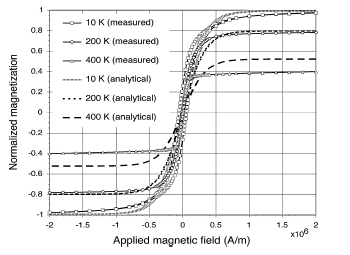
图 . 5 

在居里点为 550 K时，使用替代材料钴铁氧体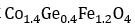的实验数据验证受温度影响的JA模型。使用 SQUID 磁力计测量磁滞回线在10K 到 400 K 区间内各种温度下的变化，并与计算的数值进行比较。通过将（5）中所示的自发磁化分析模型拟合到测量数据（见图 1），估算临界指数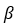为 0.4。

图 4 显示了替代材料钴铁氧体的矫顽场对温度的依赖性。正如预期的那样，矫顽力随温度呈指数衰减[10]。从图中可以看出，分析模型与测量结果非常吻合。图 5 比较了替代材料钴铁氧体在 0 K、200 K 和 400 K 温度下测量计算出的磁滞回线。随着温度接近居里点(550 K)，磁滞回线趋平。越过居里点之后，材料具有顺磁性，并且不表现出滞后现象。在较高温度下，计算出的磁滞回线开始偏离测量回线。这种行为可能是由于对该模型中域密度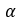与温度无关的假设，此结论并不完全正确。

四、讨论与结论

本文讨论了基于JA 理论延伸出来的模型在温度影响下的滞后效应变化。通过四个磁滞参数将热效应纳入现有模型：自发磁化强度、磁畴耦合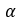,钉扎因子,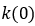和可逆性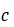，并在模型中引入居里温度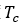和临界点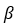作为新参数。对于所用模型的识别过程包括使用合适的算法从测量数据中提取 0 K 处的一组模型参数，并从磁化-温度曲线中找到居里温度和临界指数。如果引入不同滞后参数的不同临界指数并实现域密度的温度依赖性分析模型，则可以进一步改进模型。通过用替代材料钴铁氧体对受温度影响的JA 模型进行了测量验证。实验对比表明，受温度影响的 JA 模型与测量结果非常吻合。